Basic Logic
Review of Arguments
We have said that analytic philosophy proceeds via argument analysis. And we have said that both form and content must be carefully and charitably analyzed.
We charitably analyze content by being as crisp and clear about propositional content as possible. We seek to truly understand the content of an argument, and we try to engage with the author as thoroughly as possible. Our goal is never to “slam” an argument! Our goal is to understand the author’s intentions. However, necessarily, analyzing content has elements of subjectivity, despite our best efforts.
With inductive arguments in particular, argument-evaluation has as much art as analysis. The formal, inferential relations between premise(s) and conclusion are not “tight,” and even true premises do not guarantee a true conclusion. Induction “works,” and we are psychologically disposed to think in inductive ways. But induction does not fall to the sort of rigorous analysis we can achieve with deductive arguments.
Furthermore, even in inductive arguments, we employ logical inferences as we often build a “logical flow” through the premises to the conclusion. If these inferences are not good, then even what relation there is between premises and conclusion is weakened.
Finally, it is in deduction that we are able to become truly “strict” and reliable in our inference analysis. And, fortunately, most of the analysis of evolutionary arguments we will perform can be done via deductive argument and inferences.
So, we will now turn our attention to the basics of logic. In the process, you will learn to see the formal structures of propositional reasoning, and we will rely heavily upon deductive logic as we proceed through this course.
Logical Relations and “Connectives”
“Inferences” are simply logical relations between simple propositions. We use them all the time! For our purposes, let us assign two “sentence letters” with propositional sentences.
P: There is fire.
Q: There is heat.
These are simple propositions. There is no “logic” involved in making such simple claims.
However, we can build up complex propositions by “connecting” these propositions in various, logic-laden ways.
We could say, “There is fire, and there is heat.” We could say, “Fire causes heat.” We could say, “If there is fire, there is heat.” We could even say, “There is no fire.” And so on.
So, we can relate these simple propositions to each other in various logic-laden ways.
The questions facing logicians concern “how those logical relations work,” what we “mean” when we connect propositions into complex relations.
The “basic logic” we will do in this section of the course will use five logical connectives: not, and, or, if-then, if-and-only-if.
It is far beyond the scope of this course to be “acting logicians” and discuss how and why these connectives “work” the way they do. However, before proceeding to define these connectives, I would be irresponsible to not at least mention two things.
First, we will be employing “classical logic” throughout this course. That means primarily that we will be employing bivalent logic, using two and only two truth values: true and false. For a summary of bivalence, please read this post.
Second, I should mention what an “axiom” actually is. An axiom is a “law of logic” that is so indubitable that your own attempt to dispute it ends up appealing to it. An example is: “If P, then P,” in other words: “If there is fire, then there is fire.” Your every attempt to dispute that relation between propositions will end up appealing to that relation itself. Another example is: “If P, then if R then P,” in other words: “If there is fire, then if the moon is made of green cheese, there is still fire.”
To dispute such relations, you end up employing them. So, these are considered “basic” to classical logical thought. And, amazingly, all of the logical connectives we presently employ (and will see as extremely intuitive, because we use them all the time) can be built up from such “barren” axioms! Thus, the system of classical logic is both reliable and robust. It is sufficient for our purposes, and the sorts of inferences we will employ in this course will withstand scrutiny.
Now, let us turn our attention to the logical connectives themselves, as we define what the logical relations really mean.
Truth Functionality
We will employ truth tables to define these relations. We could alternatively use the methods of deduction to prove from the axioms that these connectives really do capture the necessary relations we define. We can also prove that the truth tables precisely cohere with the deductive results. But all of those things are beyond the scope of this course. All we really need to accomplish here is to define how “truth” works when relating propositions using these connectives.
And that is primarily what we mean by “truth functional.” Truth functionality means, in a nutshell, that propositional content is irrelevant to the truth of complex propositions. It means that we can “abstract” away from the meaning and content to simply assign truth-values to propositions, and we then define the connectives in terms of how they affect the truth value of the complex in various scenarios.
A “scenario” is just a way the world could be. If I claim, “There is fire,” there are countless ways that the world could be regarding fire. But, ultimately, all of the ways the world could be break down into two classes: In some scenarios my claim will be true, and in some scenarios my claim will be false. So, a “scenario” is just a way the world could be that would result in the truth or falsity of my claim.
So, we “abstract” away from all of the content! We don’t need to know what “P” or “Q” means or contains, because every way the world could be will still have “P” a true proposition or a false proposition. Thus, we don’t need to “do logic” with any content or “meaning” in the slightest! Everything comes down to relations between true and false, and logic itself concerns itself strictly with truth and falsity, not with “meaning” or content.
“Truth functionality,” then, just means that we are dealing strictly with truth and falsity and how that emerges in complex sentences that are connected via our logical connectives. So, truth tables are actually the perfect vehicle for defining our logical relations, because they do abstract to just the truth values as they are defined by the relations.
I have said that we will employ five logical connectives, so let us get straight to them. In what follows, I will simply give the truth tables, and there will be links to two additional pages (conditional and biconditional) to further discuss them. Particularly regarding the truth table for Conditional, please review the additional explanation page! It is critical to your understanding as we move forward in the course; you will really struggle going forward if you do not understand how Conditional works!
The Not Connective (Negation)
For negation, we will employ the following symbol: ~
We use this symbol when we are saying, “It is not the case that…,” such as: “There is no fire,” or, “It is not the case that there is fire.”
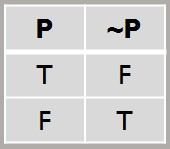
This connective is extremely intuitive. We can say, “It is not the case that…,” and when we do that, we are always just flipping the truth value of the proposition that this connective modifies.
The one thing that seems strange is to call this a “connective,” because it does not appear to be connecting anything! And sure enough, this is the one connective that we call a “unary connective,” as it “connects” only one thing. It simply modifies a single proposition.
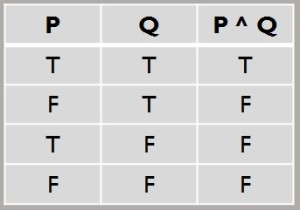
The And Connective (Conjunction)
For conjunction, we will employ the following symbol: ^
We use this symbol when we are saying, “This is the case, and that is the case,” such as: “There is fire, and there is heat.”
Like negation, conjunction is extremely intuitive. If we are really saying that P and Q are both the case, then that claim would be falsified by any scenarios in which either or both of the propositions proved to be false. The truth table captures that both P and Q must be true in order for the complex proposition to also be true.
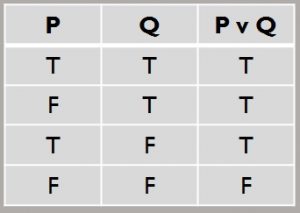
The Or Connective (Disjunction)
For disjunction, we will employ the following symbol: v
We use this symbol when we are saying, “This is the case, or that is the case,” such as: “There is fire, or there is heat.”
Disjunction is also extremely intuitive. If we are saying that either P is the case or Q is the case, then those scenarios captured by the truth table that have either one as true have the disjunctive proposition true. And in any scenario in which both P and Q are false, the claim that one or the other is true must itself be false (as the bottom row of the truth table shows). If you claim that one or the other is true, then at least one of them must indeed be true!
The one row of the table that might seem strange is the top one, the scenario where both P and Q are true. Perhaps your intuition is that of “exclusive or,” which is to say: “P or Q is the case, but not both.” This truth table establishes an “inclusive or,” which is to say: “P or Q or both is the case.”
Why do we claim that the actual logic of the relation is inclusive rather than exclusive? After all, we find countless examples in which the exclusive sense is what we mean: “You may have soup or salad.” When a waiter tells us that we may have soup or salad, we know that this is certainly intended in an exclusive sense!
Remember what we said earlier about truth-functionality? We said that the “meaning” and content (and in this case, context) are irrelevant to the relations. Notice that in our soup/salad example, you must know the context and content of the disjunctive proposition in order to know whether to take the disjunction in the exclusive or inclusive sense. So, does this mean that truth-functionality is a mistake, that somehow it isn’t properly capturing our actual logic in all cases?
There are (at least) two good responses to this question:
1) If you think about the way you use “or” most commonly, you will see that you almost always intend it in the inclusive sense. It is only in certain “artificial” contexts that we have learned to treat it in the exclusive sense. Imagine somebody coming to a restaurant for the very first time, not knowing that restaurant ‘or’s are intended exclusively. The waiter says, “You may have soup or salad,” and the new person responds, “Great! I’m feeling hungry. I’ll have both.” Would we say that the new person was being illogical? No, we would say that s/he doesn’t understand the context.
2) Even using the inclusive sense of disjunction, we can still easily capture the exclusive sense if we wish. It is not like truth functionality limits what we want to say! In fact, it forces us to be even more clear. So, we express exclusive disjunction this way: (P v Q) ^ ~(P ^ Q). In English: “P or Q, and not P and Q”. This is the symbolization of: “You may have soup or salad, but not both.” And we know from experience and context the “but not both” part.
So, disjunction is cast in the inclusive sense (the top row of the truth table), but we can easily (and more clearly) specify what we mean if we intend to use disjunction in the exclusive sense.
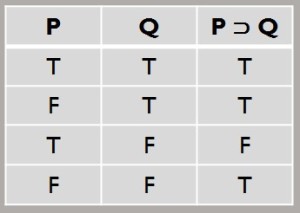
The If, Then Connective (Conditional)
For conditional, we will employ the following symbol: ⊃
We use this symbol when we are saying, “If this is the case, then that is the case,” such as: “If there is fire, then there is heat.”
There is too much to say about conditional for this one page. So, please read this additional page regarding conditional.
The If-and-Only-If Connective (Biconditional)
For biconditional, we will employ the following symbol: ≡
We use this symbol when we are saying, “If this is the case, then that is the case; and if that is the case, then this is the case,” such as: “If there is fire, then there is heat; and if there is heat, then there is fire.” This logical relation can be streamlined by saying, “This is the case if and only if that is the case,” such as: “There is fire if and only if there is heat.” We can further streamline the verbiage by contracting “if and only if” to simply “iff” (with two trailing ‘f’s), such as: “There is fire iff there is heat.”
Biconditional is just expressing two conditionals: One where P is the antecedent, and one where Q is the antecedent. So, the truth table shows that only where the “two-way conditional” would be true when overlapping two conditional truth tables is the biconditional proposition true.
Another way of saying this is that the biconditional expresses “logical equivalency”. When we say “P iff Q,” what we are really saying is that we can use P and Q interchangeably in sentences, and the truth-value of the containing sentence will remain the same. If putting P into a sentence makes that sentence false, then putting Q in its place will also produce a false sentence; and vice versa!
Biconditional is frequently used in definitions, because we can say things like “just is” with that relation: “A bachelor just is an unmarried man.” That is the same propositional content as: “A person is a bachelor iff that person is an unmarried man.”
Notice the logical equivalency in that example! Every place that I could use the word “bachelor,” I could also use the term “unmarried man.” If I have the definition correct, which is to say, if the biconditional claim is true, then “bachelor” and “unmarried man” are interchangeable in truth-preserving fashion! Philosophers use the Latin term: salva veritate, which literally means “truth preserving” or “saving truth”.
We will employ many biconditionals in this course, because of its power to rigorously capture definitions and logical equivalency.
As just one quick example, non-theist physicists are generally committed to the idea that physics just is metaphysics. They would say that there literally is nothing about reality that in principle escapes what can (or ultimately will) be explained and expressed by physics. So, the commitment is most clearly expressed with the biconditional: physics ≡ metaphysics.
Please notice how just casting the claim in biconditional terms immediately clarifies how strong the relation is supposed to be between physics and metaphysics. If philosophers are seeking anything, they are seeking clarity! Clarity is absolutely foundational to truth-seeking! And clearly understanding logic and what it implies for the relations between claims is central to that process of seeking clarity.
Thus, as we move forward, we will employ more and more symbolized logic, so that we more and more clarify exactly what we are talking about and analyzing.